Система географических координат

Способы изображения земной поверхности. Метод проекций в геодезии

_______На местности точки, линии, углы и контуры расположены в силу неровностей земной поверхности на возвышениях или впадинах. Так как возвышения и впадины являются пространственными формами, изобразить их на бумаге в виде плоской карты или плана достаточно непросто. Способы изображения земной поверхности на плоскости основываются на методе проекций.

_______При изучении действительной поверхности Земли точки местности проецируют отвесными линиями на поверхность земного эллипсоида. Так как уровенная поверхность радиусом до 20 км может быть заменена плоскостью, при относительно небольших площадях, точки местности проецируют на горизонтальную плоскость. Положение полученных проекций точек может быть определено координатами.

_______В результате перенесения точек на плоскость длины линий заменяют их горизонтальными проекциями, называемыми горизонтальными проложениями; пространственные углы заменяются плоскими, и вся фигура заменяется проекцией на горизонтальную плоскость (рис. 2).

Дистанционные курсы для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие

Время чтения: 15 минут

В Россию приехали 10 тысяч детей из Луганской и Донецкой Народных республик

Время чтения: 2 минуты

Онлайн-тренинг: нейрогимнастика для успешной учёбы и комфортной жизни

Время чтения: 2 минуты

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Студенты российских вузов смогут получить 1 млн рублей на создание стартапов

Время чтения: 3 минуты

Школы граничащих с Украиной районов Крыма досрочно уйдут на каникулы

Время чтения: 0 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

• Заполняющий дневник улетевшие на юг промелькнувший хвост написавший доклад

    

• Экономика норвегии презентация и доклад

    

• Доклад на тему свадебные обряды

    

• Бронзовый век на северном кавказе доклад 5 класс

    

• Доклад черноземные почвы богатство россии

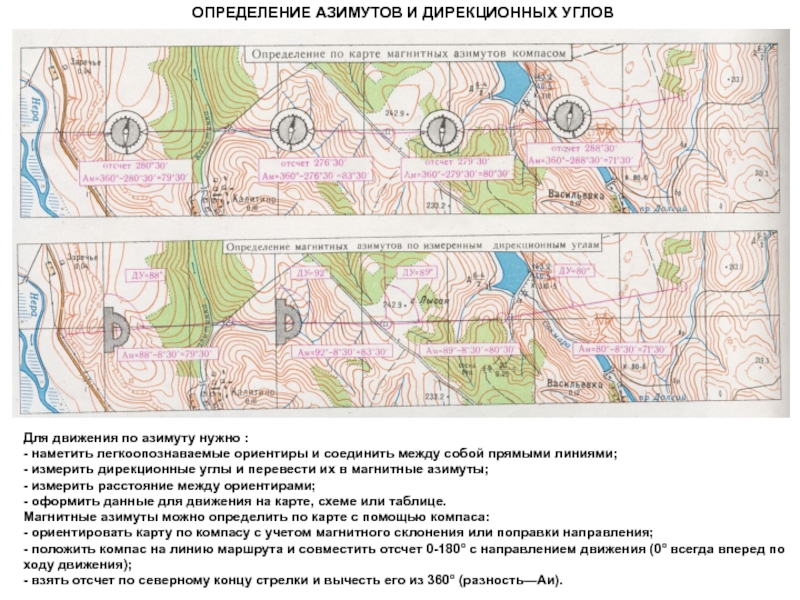
Слайд 12ОПРЕДЕЛЕНИЕ АЗИМУТОВ И ДИРЕКЦИОННЫХ УГЛОВДля движения по азимуту нужно :- наметить

легкоопознаваемые ориентиры и соединить между собой прямыми линиями;- измерить дирекционные углы и перевести их в магнитные азимуты;- измерить расстояние между ориентирами;- оформить данные для движения на карте, схеме или таблице.Магнитные азимуты можно определить по карте с помощью компаса:- ориентировать карту по компасу с учетом магнитного склонения или поправки направления;- положить компас на линию маршрута и совместить отсчет 0-180° с направлением движения (0° всегда вперед по ходу движения);- взять отсчет по северному концу стрелки и вычесть его из 360° (разность—Аи).

Декартова и полярная системы координат

Декартова система координат

Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке.

Точка пересечения осей называется началом координат, а сами оси — координатными осями. Первая из координатных осей называется осью абсцисс, вторая — осью ординат.

• Начало координат обозначается буквой О, ось абсцисс — символом Ох, ось ординат — символом Оу.
• Координатами произвольной точки М в заданной системе называют числа
• , 

( см. рис. 1), где  и  суть проекции точки М на оси Ох и Оу,  обозначает величину отрезка  оси абсцисс,  — величину отрезка  оси ординат. Число х называется абсциссой точки М, число у — ординатой этой же точки. Символ М(х; у) обозначает, что точка М имеет абсциссой число х, а ординатой число у.

Ось Оу разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Ох, называется правой, другая — левой. Точно так же ось Оу разделяет плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Оу, называется верхней, другая нижней.

Обе координатные оси вместе разделяют плоскость на четыре четверти, которые нумеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй — лежащая в левой и в верхней полуплоскости, третьей — лежащая в левой и в нижней полуплоскости, четвертой — лежащая в правой и в нижней полуплоскости.

Полярна система координат

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча ОА, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Полярными координатами произвольной точки М (относительно заданной системы) называются числа  и  (см. рис.). Угол  при этом следует понимать так, как принято в тригонометрии. Число  называется первой координатой, или полярным углом точки М ( называются также амплитудой).

Символ М(; ) обозначает, что точка М имеет полярные координаты  и .

Полярный угол  имеет бесконечно много возможных значений (отличающихся друг от друга на величину вида , где n — целое положительное число). Значение полярного угла, удовлетворяющее неравенствам , называется главным.

В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1). Пользоваться одним и тем же масштабом, 

2).

При определении полярных углов считать положительным повороты в том направлении, в каком следует вращать положительную ось абсцисс, чтобы кратчайшим путем совместить ее с положительной осью ординат (таким образом, если оси декартовой системы находятся в обычном расположении, то есть ось Ох направлена вправо, а ось Оу — вверх, то и отсчет полярных углов должен быть обычным, то есть положительными следует считать те углы, которые отсчитываются против часовой стрелки).

1. При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки х к декартовым координатам той же точки осуществляется по формулам
2. , .
3. В этом же случае формулы
4. , 
5. являются формулами перехода от декартовых координат к полярным.
6. При одновременно рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштаб для обеих систем одинаковыми.

Географические координаты некоторых городов России и стран СНГ

Город	Широта	Долгота
Абакан	53.720976	91.44242300000001
Архангельск	64.539304	40.518735
Астана (Казахстан)	71.430564	51.128422
Астрахань	46.347869	48.033574
Барнаул	53.356132	83.74961999999999
Белгород	50.597467	36.588849
Бийск	52.541444	85.219686
Бишкек (Киргизия)	42.871027	74.59452
Благовещенск	50.290658	127.527173
Братск	56.151382	101.634152
Брянск	53.2434	34.364198
Великий Новгород	58.521475	31.275475
Владивосток	43.134019	131.928379
Владикавказ	43.024122	44.690476
Владимир	56.129042	40.40703
Волгоград	48.707103	44.516939
Вологда	59.220492	39.891568
Воронеж	51.661535	39.200287
Грозный	43.317992	45.698197
Донецк (Украина)	48.015877	37.80285
Екатеринбург	56.838002	60.597295
Иваново	57.000348	40.973921
Ижевск	56.852775	53.211463
Иркутск	52.286387	104.28066
Казань	55.795793	49.106585
Калининград	55.916229	37.854467
Калуга	54.507014	36.252277
Каменск-Уральский	56.414897	61.918905
Кемерово	55.359594	86.08778100000001
Киев (Украина)	50.402395	30.532690
Киров	54.079033	34.323163
Комсомольск-на-Амуре	50.54986	137.007867
Королев	55.916229	37.854467
Кострома	57.767683	40.926418
Краснодар	45.023877	38.970157
Красноярск	56.008691	92.870529
Курск	51.730361	36.192647
Липецк	52.61022	39.594719
Магнитогорск	53.411677	58.984415
Махачкала	42.984913	47.504646
Минск (Беларусь)	53.906077	27.554914
Москва	55.755773	37.617761
Мурманск	68.96956299999999	33.07454
Набережные Челны	55.743553	52.39582
Нижний Новгород	56.323902	44.002267
Нижний Тагил	57.910144	59.98132
Новокузнецк	53.786502	87.155205
Новороссийск	44.723489	37.76866
Новосибирск	55.028739	82.90692799999999
Норильск	69.349039	88.201014
Омск	54.989342	73.368212
Орел	52.970306	36.063514
Оренбург	51.76806	55.097449
Пенза	53.194546	45.019529
Первоуральск	56.908099	59.942935
Пермь	58.004785	56.237654
Прокопьевск	53.895355	86.744657
Псков	57.819365	28.331786
Ростов-на-Дону	47.227151	39.744972
Рыбинск	58.13853	38.573586
Рязань	54.619886	39.744954
Самара	53.195533	50.101801
Санкт-Петербург	59.938806	30.314278
Саратов	51.531528	46.03582
Севастополь	44.616649	33.52536
Северодвинск	64.55818600000001	39.82962
Северодвинск	64.558186	39.82962
Симферополь	44.952116	34.102411
Сочи	43.581509	39.722882
Ставрополь	45.044502	41.969065
Сухум	43.015679	41.025071
Тамбов	52.721246	41.452238
Ташкент (Узбекистан)	41.314321	69.267295
Тверь	56.859611	35.911896
Тольятти	53.511311	49.418084
Томск	56.495116	84.972128
Тула	54.193033	37.617752
Тюмень	57.153033	65.534328
Улан-Удэ	51.833507	107.584125
Ульяновск	54.317002	48.402243
Уфа	54.734768	55.957838
Хабаровск	48.472584	135.057732
Харьков (Украина)	49.993499	36.230376
Чебоксары	56.1439	47.248887
Челябинск	55.159774	61.402455
Шахты	47.708485	40.215958
Энгельс	51.498891	46.125121
Южно-Сахалинск	46.959118	142.738068
Якутск	62.027833	129.704151
Ярославль	57.626569	39.893822

Для чего нужна широта и долгота

Передвигаясь по бескрайнему океану или не менее обширной пустыне, где сложно найти указатели и ориентиры, тяжело определиться с местоположением на местности. И в этом случае широта и долгота обеспечат возможность найти любой объект в любой точке поверхности планеты.

Система координат активно применяется в поисковых системах и картах, в навигации и даже в привычным многим географических картах, геодезических приборах, системах позиционирования и столь полюбившимся многим GPS-навигаторах либо других инструментах, которые требуются для установления расположения объекта.

Определяем географические координаты

Градусная сеть поможет определить географические координаты. Поскольку мы имеем дело с дугами и окружностями, то все расчеты координат следует производить в градусах, минутах и секундах. Поэтому и сеть называется градусной.

Градусная сеть позволяет определять местоположение любой точки на земной поверхности с помощью географических координат – широты и долготы. При определении географических координат Земля принимается за шар, хотя мы помним, что она геоид.

Географическая широта φ – угол между плоскостью экватора и отвесной линией в данной точке, другими словами – это угловое расстояние точки от экватора по меридиану. Измеряется от 0 (экватор) до 90° (полюса). Различают северную (лежащую в Северном полушарии) и южную (расположенную в Южном полушарии) широту. Северную широту принято считать положительной, а южную – отрицательной. О широтах, близких к экватору, принято говорить как о низких, к полюсам – как о высоких.

Все точки, лежащие на одной параллели, имеют одинаковую широту. На глобусе параллели подписываются на 0° и 180° меридианах, на картах – на боковых рамках.

Определение географической широты

Все параллели – окружности, они содержат 360°. От экватора до каждого из полюсов градусное расстояние составляет 90°.

Ответьте на вопросы. По какой параллели можно быстрее совершить кругосветное путешествие – по 0° или по 66°?  Почему кругосветные плавания нельзя считать доказательством шарообразности Земли?

«… 7июня 1862 г. трёхмачтовое судно «Британия» … Глазго потерпело крушение …гони … южн… берег… два матроса Капитан Гр… дости… контин… пл… жесток… инд… брошен этот документ … долготы и 37° … широты. Окажите им помощь… погибнут …» — это всё, что было известно о гибели судна капитана Гранта из романа Жюля Верна «Дети капитана Гранта». Но одной широты недостаточно, чтобы определить положение объекта на Земле. Ведь 37 параллель только в Южном полушарии пересекает и Южную Америку, и Австралию, и Новую Зеландию, и многочисленные острова.

Географическая долгота λ – двугранный угол, образованный плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку, иначе – угловое расстояние точки от начального меридиана.

Все меридианы – дуги и по длине они одинаковые. Поэтому люди договорились, от какого из них вести отсчёт. Долгое время каждая страна вела счёт долготы от своего начального меридиана, Франция – от Парижского, Россия – от Пулковского (с обсерваторией) у Санкт-Петербурга, США и Англия – от Гринвичского. С 1884 года нулевым и начальным меридианом для всех стран считается Гринвичский. Он проходит через пригород города Лондона Гринвич, где в 1637 г была основана одна из старейших в мире астрономических обсерваторий. Выбор начального меридиана очень важен, так как с ним связан и отсчёт времени.

От нулевого меридиана ведут счёт расстояния в градусах на восток от 0° до 180° и на запад 0° до 180°. Нулевой меридиан, продолжением которого является 180°, делит Землю на Западное и Восточное полушария. Меридианы показывают направление север-юг.

К востоку от Гринвичского меридиана долгота восточная, к западу – западная. От неё зависит местное солнечное время. Все точки, лежащие на одном меридиане, имеют одинаковую долготу. На глобусе меридианы подписываются на экваторе, на картах – на экваторе или на верхней и нижней рамках. На практике географическую долготу определяют по разнице местного времени между нулевым меридианом и меридианом пункта наблюдения.

Определение географической долготы

Любая точка на земле имеет свой «географический адрес». Теперь мы знаем, что этот адрес состоит из двух частей. Это как при игре в «морской бой», где тоже используется адрес. Две части географического адреса – широта и долгота, определить их нам помогает градусная сеть. Широта – место точки на определённой параллели, долгота – на меридиане. Место их пересечения и есть географический адрес – географические координаты.

Зная географические координаты можно найти любой объект на карте. И, наоборот, можно нанести новый объект на карту, определив его географические координаты, как это делали все первооткрыватели. Ошибки в этом стоили многих жизней.

До времени существования навигаторов, географические координаты в открытом море определяли сначала с помощью такого прибора, как астролябия, а затем его заменил секстант.

АстролябияСекстант

Деление отрезка в заданном отношении.

Найдем координаты точки \(M\) на отрезке \(AB\), которая делит этот отрезок в отношении \(\lambda/\mu\), то есть удовлетворяет условию
$$
\frac{|AM|}{|MB|} = \frac{\lambda}{\mu},\ \lambda > 0,\ \mu > 0\nonumber
$$
(рис. 2.3). Это условие можно переписать в виде
$$
\mu\overrightarrow{AM} = \lambda\overrightarrow{MB}.\label{ref1}
$$

Рис. 2.3

Обозначив через (\(x_{1}\), \(y_{1}\), \(z_{1}\)) и (\(x_{2}\), \(y_{2}\), \(z_{2}\)) соответственно координаты точек \(A\) и \(B\), а через (\(x\), \(y\), \(z\)) координаты точки \(M\), разложим обе части равенства по базису, причем компоненты векторов \(\overrightarrow{AM}\) и \(\overrightarrow{MB}\) найдем по . Тогда
$$
\mu(x-x_{1}) = \lambda(x_{2}-x),\ \mu(y-y_{1}) = \lambda(y_{2}-y),\ \mu(z-z_{1}) = \lambda(z_{2}-z).\nonumber
$$
Из этих равенств можно найти \(x\), \(y\) и \(z\), поскольку \(\lambda + \mu \neq 0\):
$$
x = \frac{\mu x_{1} + \lambda x_{2}}{\lambda + \mu},\ y = \frac{\mu y_{1} + \lambda y_{2}}{\lambda + \mu},\ z = \frac{\mu z_{1} + \lambda z_{2}}{\lambda + \mu}\label{ref2}
$$
Если в формулах \eqref{ref2} мы будем считать одно из чисел \(\lambda\) или \(\mu\) отрицательным, то из равенства \eqref{ref1} увидим, что \(M\) находится на той же прямой вне отрезка \(AB\), деля его в отношении |\(\lambda/\mu\)|. Поэтому из формул \eqref{ref2} можно найти координаты точки, делящей отрезок в заданном отношении как внутренним, так и внешним образом.

На плоскости и на прямой линии задача о делении отрезка решается точно так же, только из трех равенств в \eqref{ref2} остается соответственно два и одно равенство.

Как найти координаты искомой точки

Часто встаёт вопрос, как следует определять широту и долготу по карте, если нужная точка, удалённая от сетки координат, находится внутри квадрата.

Вычисление координат затруднено также тогда, когда изображение местности имеет огромный масштаб, а более подробного с собой нет.

• Здесь без специальных вычислений не обойтись — понадобятся линейка с карандашом или циркуль.
• Вначале определяются ближайшие параллель и меридиан.
• Фиксируется их цифровое обозначение, затем — шаг.
• Далее от каждой из дуг измеряется расстояние в миллиметрах, затем переводится в километры с помощью масштаба.
• Всё это соотносится с шагом параллелей, а также шагом меридианов, нанесенных в определённом масштабе.
• Есть изображения с разным шагом — 15º, 10º, а есть меньше 4º, это напрямую зависит от масштаба.
• Узнав между ближайшими дугами расстояние, также значение в градусах, нужно вычислить разницу, на сколько градусов заданный пункт отклонен от сетки координат.
• Параллель — если объект в северном полушарии, то к меньшей цифре полученную разницу прибавляем, от большей — отнимаем, для южного это правило действует аналогично, только вычисления проводим, как с положительными числами, но конечная цифра будет отрицательной.
• Меридиан — положение заданной точки в восточном либо западном полушарии на исчисления не влияет, к меньшему значению параллели прибавляем свои расчёты, от большей — отнимаем.

Циркулем тоже несложно вычислить географическое местоположение — чтобы получить значение параллели, его концы нужно поставить на точку нужного объекта и ближайшую горизонтальную дугу, а затем распор циркуля перенести на масштаб имеющейся карты. А чтобы узнать величину меридиана, всё это повторить с ближайшей вертикальной дугой.

Для оформления выписки из ЕГРН найдите ваш объект по адресу или по кадастровому номеру:

Сведения из Росреестра

Кликните на карте на любой земельный участок

Как узнать координаты кадастрового участка? Это легко сделать, если знать его номер. Этот уникальный код есть у каждого объекта недвижимости, прошедшего регистрацию. Чтобы определить координаты по кадастровому номеру, используется карта. Следует ввести код в специальное поле, чтобы открылся перечень данных о недвижимости.

Кроме точных координат, по кадастровому номеру можно узнать адрес участка, его предназначение, и многое другое. Иными словами, удается получить полную информацию. Почему так происходит? Дело в том, что кадастровый номер является индивидуальным параметром объекта недвижимости. То есть, определенное числовое значение присвоено только ему. Для других объектов оно не повторяется. Это означает, что получится найти только участок, соответствующий указанному номеру.

Координаты участка по кадастровому номеру определяются быстро, если применить кадастровую карту онлайн. Она хранит данные, которые полностью соответствуют действительности. Все участки размещены в точной очередности, все границы соблюдены. Другими словами, отображается реальная территория со всеми объектами недвижимости, но представленная в масштабе. Что бы узнать координаты кадастрового участка, нужно заказать выписку из ЕГРН.

Вторая экваториальная система координат

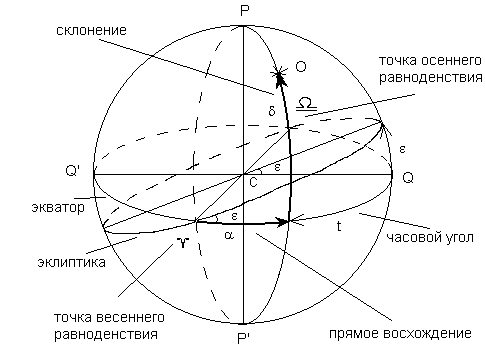
Что интересно, главная плоскость и точка отчёта аналогичны предыдущей системе. Но её координатами выступают склонение и прямое восхождение. Подразумевается, что восхождение это дуга экватора неба, которая проходит от точки весеннего равноденствия до круга светила. Кроме того, измерение проходит в часовой мере. Однако, её отсчёт ведётся противоположно часовой стрелки. Между тем, вторая система координат, характеризуется постоянными координатами звёзд. В противовес первой системе, движение Земли за сутки не влияет на них. Применяется она для определения перемещения небесных тел за год.

Вторая экваториальная система координат

Важно понимать, что координаты могут быть всегда разными. Поэтому существует множество задач

Их решение возможно с применением, подходящей отдельной ситуации, системой. Вообще, для решения задач и определении координат, очень часто чередуют системы.

Создание систем координат позволило учёным составить карту звёздного неба. Кроме того, обрисовалась определённая структура небесной системы. Что, в значительной мере, способствовало развитию астрономии и астрологии. Помимо того, экваториальные системы координат применяются во многих областях научной деятельности.

Звёздное небо

Очевидно, что разработка и внедрение определённых систем, составляет основу исследования космического пространства. Мы стараемся максимально приблизиться к его пониманию. Конечно, множество уже применяемых приёмов, расчётов и методов способствует расширению нашего кругозора.

Как определить прямоугольные координаты точек на топографической карте?

Плоские прямоугольные координаты. При определении полных координат точки по оцифровке координатной линии, образующей южную сторону квадрата, в котором расположена точка, находят и записывают полное значение абсцисс х в километрах.

Как узнать прямоугольные координаты?

Прямоугольные координаты определяют с помощью координатной (километровой) сетки, представляющей собой сеть линий, параллельных экватору и осевому меридиану зоны.

Как определить географические и прямоугольные координаты точки на карте?

Прямоугольные координаты точки (х, у) по карте определяются с помощью километровой сетки. Абсциссы х, началом отсчета которых принимается линия экватора, подписаны у горизонтальных линий полностью только в углах рамки. В остальном указываются только две последние цифры, называемые сокращёнными координатами.

Что такое плоские прямоугольные координаты?

Прямоугольные координаты (плоские) — линейные величины: абсцисса Х и ордината Y, определяющие положение точек на плоскости (на карте) относительно двух взаимно перпендикулярных осей Х и Y (рис. 14).

Как на карте определить плоские прямоугольные координаты?

С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить плоские прямоугольные координаты любой точки на карте. С точностью до километра. Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М, и прочитать цифры, обозначающие данный квадрат.

  Как можно определить диаметр мяча?

Каковы размеры сетки квадратов прямоугольных координат на плане?

Сетку квадратов, в зависимости от масштаба плана, строят размерами 40 х 40 см или 50 х 50 см со стороной квадрата 10 см. … Контроль построения сетки квадратов выполняется проверкой диагоналей каждого квадрата одним раствором циркуля-измерителя, равным 141,4 мм. Разности диагоналей не должны быть более 0,2 мм.

Как определить широту и долготу на карте?

Важно: Географическая долгота измеряется от 0 до 180°. Чтобы определить географическую широту, нужно от заданной точки провести воображаемую прямую вдоль ближайшей параллели

Это и будет географическая широта. Она будет указана сбоку на карте.

Как определить географические координаты точки на карте?

Географические координаты точки, расположенной на карте, определяют от ближайших к ней параллели и меридиана, широта и долгота которых известна. Рамка топографической карты разбита на минуты, которые разделены точками на деления по 10 секунд в каждом.

Какие координаты бывают?

Основные системы

• Декартовы координаты
• Полярные координаты
• Цилиндрические координаты
• Сферические координаты
• Декартовы и полярные
• Декартовы и цилиндрические
• Декартовы и сферические
• Цилиндрические и сферические