Плоские прямоугольные координаты, как определить плоские прямоугольные координаты по топографической карте

Вычисление площади и высоты

Рассмотрим типовую задачу, встречающуюся в экзаменационных работах. Даны точки с ординатами A (-2, -3); B (-3,4); C (4,5). Необходимо выполнить построение фигуры, найти её площадь и доказать, что угол A равный C.

Если отложить данные точки на плоскости и соединить их, то получится треугольник. Взяв за тождество, что углы A и C равны, можно сделать предположение о равнобедренности треугольника. Это значит, что две его стороны имеют одинаковую длину. Длина стороны AB — это отрезок A и B с заданными координатами. Поэтому равна она будет следующему выражению: AB = ((-2 + 3)2 + (-3 — 4)2)½ = (1 +49)½ = (50)½. По аналогии находится длина другой стороны: BC = ((-3 — 4)2 + (4 — 5)2)½ = 2 = (1 +49)½ = (50)½.

Для того чтобы найти площадь треугольника, используется правило, что она находится умножением высоты на длину стороны, к которой проведена, и делением полученного результата на два: S = h*a/2 = BH * AC /2, где H — точка пересечения высоты и основания.

В равнобедренном треугольнике высота является биссектрисой и медианой, поэтому H лежит на середине отрезка AC. Чтобы найти её положение, используют формулу нахождения координат середины отрезка: H (x, y): X = (-2+4) /2 = 1, Y = (-3+5) / 2 = 1. Искомая точка имеет координаты H (1,1).

Высота находится как корень квадратный из двух точек: BH = ((-3−1)2 + (4−1)2)½ = (16+9)½ = 5. Теперь нужно найти основание треугольника AC. Разницы, из какой координаты вычитать другую, нет, так как результат учитывается по модулю. Основание будет равно: AC = ((-2−4)2 + (-3−5)2)½ = (36 + 64)½ = 10. Полученные значения высоты и основания подставляют в формулу нахождения площади и получают, что она равна: S = 5*10/2 = 25. Задача решена.

Указание какого-либо объекта на топографической карте с помощью плоских прямоугольных координат.

Для указания какого-либообъекта на карте обычно говорят так: точка М находится в квадрате 50 448 384, то есть называют координаты ее подряд, не разделяя их, но чаще дают указания сокращенно, называют только две последующие цифры из плоских прямоугольных координат данной точки — квадрат 4484.

Называя этот квадрат на карте, мы указываем координаты левого нижнего его угла. То есть юго-западного угла квадрата, в котором расположена точка М. Если необходимо указать более точное положение точки внутри этого квадрата, то дополнительно определяют ее расстояние от граничных линий этого квадрата. Используя масштаб, переводят эти расстояния в метры и приписывают их к цифрам обозначенного квадрата.

Например, точка М имеет следующие координаты: х = 44 500 метров, а у = 84 500 метров. Это и будут сокращенные координаты для точки М, а полные плоские прямоугольные координаты для нее запишутся так: х = 5 044 500 м, у — 384 500 м.

Нанесение точек на карту по известным плоским прямоугольным координатам производится в обратной последовательности. Сначала отбрасываются три последние цифры в координатах и находятся линии километровой сетки. То есть квадрат, в котором расположена точка. Затем, с помощьюлинейки, масштаба и циркуля, наносятся точные координаты данной точки в этом квадрате.

Определение дирекционных углов

При известном значении дирекционного угла (\(\alpha \)) одной стороны и горизонтального (\(\beta \)) можно определить значение следующей стороны:

\(\alpha _{n+1}=\alpha _{n}+\eta \)

\(\eta =180^{\circ}-\beta _{пр}\)

\(\beta _{пр}\)– значение правого по ходу угла, из чего следует:

\(\alpha _{n+1}=\alpha _{n}+180^{\circ}-\beta _{пр}\)

Для левого (\(\beta _{лев}\)) эти знаки будут противоположными:

\(\alpha _{n+1}=\alpha _{n}-180^{\circ}+\beta _{лев}\)

Поскольку значение дирекционного угла не может быть больше, чем \(360^{\circ}\), то из него, соответственно, отнимают \(360^{\circ}\). В случае с отрицательным углом, необходимо к предыдущему \(\alpha \) добавить \(180^{\circ}\) и отнять значение \(\beta _{испр}\).

Определение прямоугольных координат точек. Нанесение на карту точек по их координатам

По координатной сетке с помощью циркуля (линейки) можно:1. Определить прямоугольные координаты точки на карте.
Например, точки В (рис. 2).Для этого надо:

· записать X — оцифровку нижней километровой линии квадрата, в котором находится точка В, т.е. 6657 км;

· измерить по перпендикуляру расстояние от нижней километровой линии квадрата до точки В и, пользуясь линейным масштабом карты, определить величину этого отрезка в метрах;

· сложить измеренную величину 575 м с значением оцифровки нижней километровой линии квадрата: X=6657000+575=6657575 м.

Определение ординаты Y производят аналогично:

· записать значение Y — оцифровку левой вертикальной линии квадрата,т.е.7363;

· измерить по перпендикуляру расстояние от этой линии до точки В, т.е.335 м;

· прибавить измеренное расстояние к значению оцифровки Y левой вертикальной линии квадрата: Y=7363000+335=7363335 м.

2. Нанести на карту цель по заданным координатам.
Например, точку Г по координатам: Х=6658725 Y=7362360.Для этого надо:

· найти квадрат, в котором расположена точка Г по значению целых километров, т.е. 5862;

· отложить от левого нижнего угла квадрата отрезок в масштабе карты, равный разности абсциссы цели и нижней стороны квадрата — 725 м;

· — от полученной точки по перпендикуляру вправо отложить отрезок, равный разности ординат цели и левой стороны квадрата, т.е. 360 м.

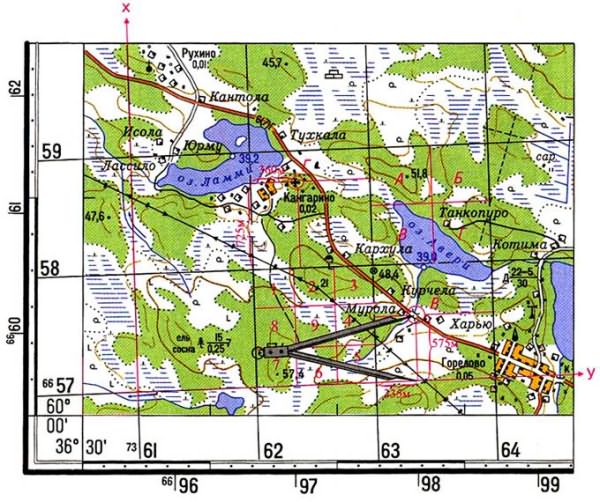Рис. 2. Определение прямоугольных координат точки по карте (точка В) и нанесение на карту точки по прямоугольных координатам (точка Г)

studopedia.ru

Разновидности теодолитных ходов

Ходы могут образовывать целые сети, пересекаясь между собой и охватывая значительные территории, а их форма определяется особенностями местности. Их принято разделять на: – замкнутый (полигон); – разомкнутый; – висячий; – диагональный (прокладывают внутри других ходов).Если необходимо заснять ровный участок, вроде строительной площадки, лучшим выбором будет полигон. На объектах вытянутого типа, вроде автодорог, принято использовать разомкнутый ход, а висячий – для съемки закрытой местности, вроде глухих улиц.

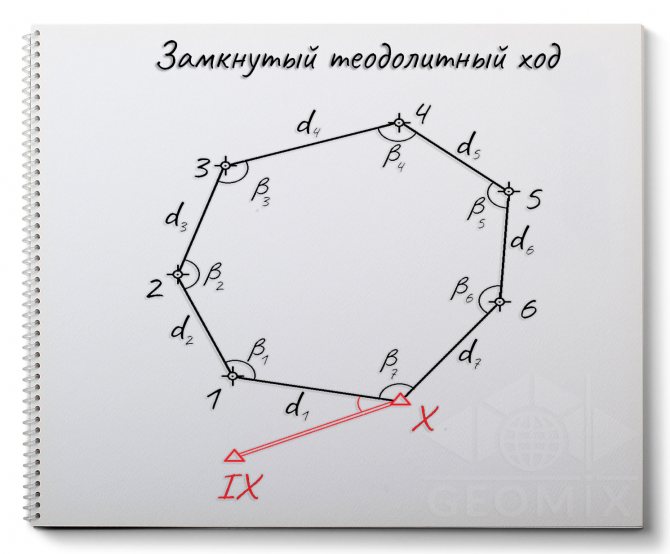
Замкнутый ход по своей сути является многоугольной фигурой и опирается только на один базовый пункт с установленными координатами и дирекционным углом. Вершинами стороны выступают точки, закрепленными на местности, а отрезками – расстояние между ними. Его чаще всего создают для съемки стройплощадок, жилых зданий, промышленных сооружений или земельных участков.

Слайд 3 Географические координаты (град.) представляют собой угловые величины (широту и долготу), которые

определяют искомой положение точки относительно экватора и меридиана, принятого за начальныйГеографическая широта (φ) — угол между отвесной линией в данной точке и плоскостью экватора. Экватор  — воображаемая линия пересечения с поверхностью Земли плоскости, перпендикулярной оси вращения и проходящей через её центр, длиной 40 075 км, служит началом отсчёта географической широты. Географическая долгота (λ) — двухгранный угол  между плоскостью начального меридиана и плоскостью меридиана данной точки земной поверхности. Меридиан — половина линии сечения поверхности земного шара плоскостью, проведённой через какую-либо точку земной поверхности и ось вращения Земли. Каждый меридиан пересекается со всеми остальными в двух точках: на Северном и Южном полюсах. Длина каждого меридиана равна 20 004 км. Все точки одного меридиана имеют одинаковую долготу, но разную широту. За начальный меридиан принят Гринвичский, проходящий через Гринвич (округ на ю-в Лондона). От него ведётся счёт долгот, согласно решению Международной меридианной конференции 1884 г.

Как определить прямоугольные координаты точек на топографической карте?

Плоские прямоугольные координаты. При определении полных координат точки по оцифровке координатной линии, образующей южную сторону квадрата, в котором расположена точка, находят и записывают полное значение абсцисс х в километрах.

Как узнать прямоугольные координаты?

Прямоугольные координаты определяют с помощью координатной (километровой) сетки, представляющей собой сеть линий, параллельных экватору и осевому меридиану зоны.

Как определить географические и прямоугольные координаты точки на карте?

Прямоугольные координаты точки (х, у) по карте определяются с помощью километровой сетки. Абсциссы х, началом отсчета которых принимается линия экватора, подписаны у горизонтальных линий полностью только в углах рамки. В остальном указываются только две последние цифры, называемые сокращёнными координатами.

Что такое плоские прямоугольные координаты?

Прямоугольные координаты (плоские) — линейные величины: абсцисса Х и ордината Y, определяющие положение точек на плоскости (на карте) относительно двух взаимно перпендикулярных осей Х и Y (рис. 14).

Как на карте определить плоские прямоугольные координаты?

С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить плоские прямоугольные координаты любой точки на карте. С точностью до километра. Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М, и прочитать цифры, обозначающие данный квадрат.

  Как можно определить диаметр мяча?

Каковы размеры сетки квадратов прямоугольных координат на плане?

Сетку квадратов, в зависимости от масштаба плана, строят размерами 40 х 40 см или 50 х 50 см со стороной квадрата 10 см. … Контроль построения сетки квадратов выполняется проверкой диагоналей каждого квадрата одним раствором циркуля-измерителя, равным 141,4 мм. Разности диагоналей не должны быть более 0,2 мм.

Как определить широту и долготу на карте?

Важно: Географическая долгота измеряется от 0 до 180°. Чтобы определить географическую широту, нужно от заданной точки провести воображаемую прямую вдоль ближайшей параллели

Это и будет географическая широта. Она будет указана сбоку на карте.

Как определить географические координаты точки на карте?

Географические координаты точки, расположенной на карте, определяют от ближайших к ней параллели и меридиана, широта и долгота которых известна. Рамка топографической карты разбита на минуты, которые разделены точками на деления по 10 секунд в каждом.

Какие координаты бывают?

Основные системы

• Декартовы координаты
• Полярные координаты
• Цилиндрические координаты
• Сферические координаты
• Декартовы и полярные
• Декартовы и цилиндрические
• Декартовы и сферические
• Цилиндрические и сферические

Общие понятия о системах координат в геодезии

Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.

Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:

1. Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
2. Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.

Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.

Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.

Нахождение угла

Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:

• записать уравнения плоскостей;
• составить векторы нормали;
• вычислить значение косинуса угла между поверхностями.

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.

Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:

{A + 0 +C + 1 = 0;

{0 + 0 + C + 1 = 0;

{A + B + 0 + 1 = 0.

Из второго равенства можно определить C. Подставив найденное C в первое равенство, можно выразить A, а после найти B. Таким образом, решением системы будет A = 0, B = -1, C = -1. Вектор нормали, соответственно, будет: N1 (0; -1; -1).

Чтобы составить уравнение второй плоскости, нужно найти координаты лишь С1. Исходя из условия, они будут равны С1 (0; 1; 1), а A и D уже известны. Подставляя данные в уравнение Ax+By+Cz+1 = 0, опять составляют систему и находят её коэффициенты. После решения второй матрицы, например, методом разложения, можно записать координаты второго вектора: N2 (-½; ½; -½).

Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2½ * ¾½) = 1 / (6½/2) = 2/6½ = 6½ / 3. Соответственно, угол равен: α = arccos = 6½ / 3.

Как определить плоские прямоугольные координаты по топографической карте.

Чтобы можно было определить плоские прямоугольные координаты точек в каждой зоне Гаусса на топографическихкартах наносится прямоугольная сетка координат, то есть проводятся линии, параллельные осевому меридиану и экватору.

Эти прямые линии, естественно, не будут совпадать с линиями, изображающими меридианы и параллели. За исключением осевого меридиана и экватора, параллельно которым они проводятся. Эту сетку координат называют километровой, так как ее линии проводятся через километр длямасштабов 1:10 000, 1:25 000, 1:50 000.

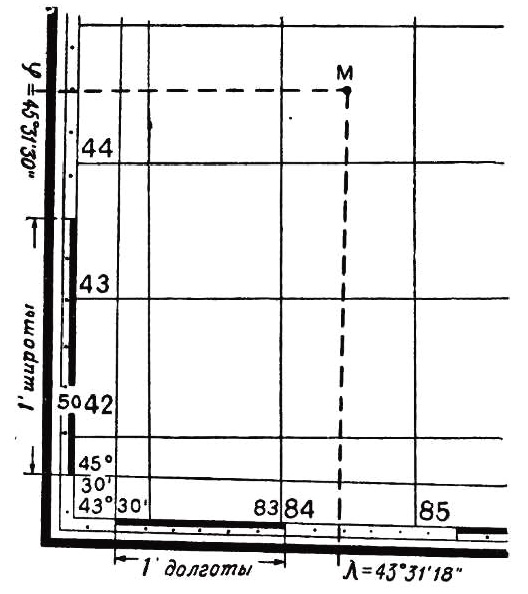
На каждом листе карты вдоль внутренней рамки даются значения координат километровой сетки от осевого меридиана данной зоны и от экватора. Значения полных координат подписываются только у крайних (верхней и нижней) линии сетки координат. У всех же промежуточных линий подписываются сокращенные обозначения, то есть только последние две цифры (десятки и единицы километров).

Например, нижняя линия километровой сетки на рисунке имеет обозначение 5042, а следующая над ней линия сетки обозначена только цифрой 43 км, а не 5043. Цифры километровой сетки под южной и над северной рамкой листа карты обозначают ординаты (у) этих линий. Крайние линии также обозначены полными координатами. Но в отличие от горизонтальных линий, первая цифра у ординат обозначает номер зоны.

Например, ордината у = 8384 км. Это значит, что лист данной карты расположен в восьмой шестиградусной зоне Гаусса, то есть ограниченной 42 и 48 меридианами восточной долготы, а точки, лежащие на линии у = 384, расположены слева от осевого меридиана на расстоянии 500-384=116 км.

С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить плоские прямоугольные координаты любойточки на карте. С точностью до километра. Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М, и прочитать цифры, обозначающие данный квадрат. Сначала обычно называется (записывается) значение координаты х — 5044, а затем у = 8384.

8.Определение географических и прямоугольных координат по карте, отметок точек по горизонталям.

Определение прямоугольных координат точки по карте

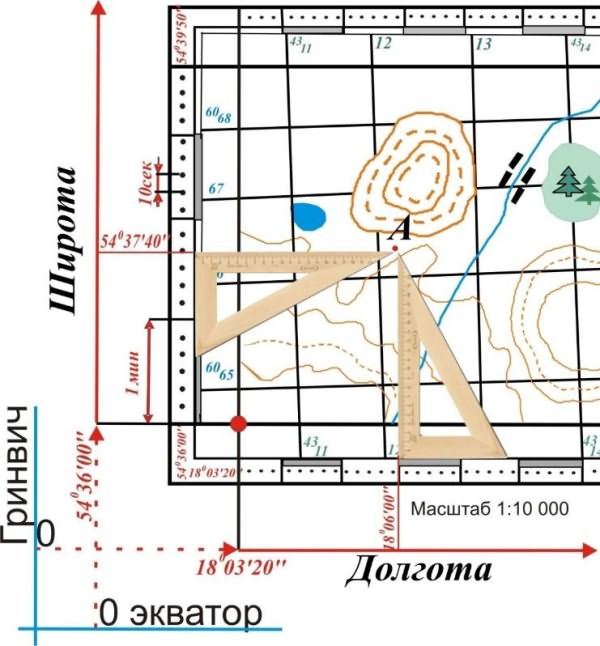
Для определения широты необходимо при помощи треугольника опустить перпендикуляр из точки А на градусную рамку на линию широты и прочитать справа или слева по шкале широты, соответствующие градусы, минуты, секунды. φА= φ0+ Δφ

φА=54036/00//+0001/40//=54037/40//

Для определения долготы необходимо при помощи треугольника опустить перпендикуляр из точки А на градусную рамку линии долготы и прочитать сверху или снизу соответствующие градусы, минуты, секунды.

Определение прямоугольных координат точки по карте

Прямоугольные координаты точки (Х, У) по карте определяют в квадрате километровой сетки следующим образом:

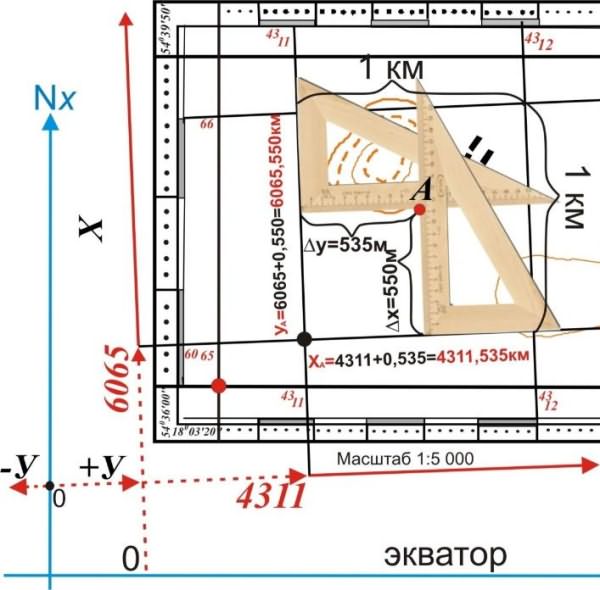
1. При помощи треугольника опускают перпендикуляры из точки А на линию километровой сетки Х и У снимаются значения ХА=Х0+ΔХ; УА=У0+ΔУ

Например, координаты точки А равны: ХА= 6065км + 0,55 км = 6065,55 км;

УА= 4311 км + 0,535 км = 4311,535 км. (координата является приведенной);

Точка А расположена в 4-ой зоне, на что указывает первая цифра координаты у приведенной.

Классификация топографических карт по масштабу

Масштаб — это понятие, отражающее разницу между расстояниями, отображёнными картографом на топосъемке участка земли, и реальным расстоянием на местности. В картографии выделяют три разновидности масштаба:

• Численный масштаб отображается на картах как дробь. Обязательным условием валидности такого масштаба будет отражение как в числителе, так и в знаменателе данных в одинаковых единицах измерения. Так, если вы увидите на карте, что она представляет собой топографическую съёмку масштаба 1:500, это означает, что в одном сантиметре на карте будет отображено пятьсот сантиметров на реальной местности.
• Именованный масштаб всегда берёт за единицу измерения один сантиметр на карте и относительно него объясняет, какое действительное расстояние на участке местности в нём отображено. Соответственно, топографическая съёмка 1:500 в именованном масштабе будет записана так: топосъёмка, в 1 см = 5 м.
• Графический масштаб выглядит как линейка, которая, согласно инструкции по составлению карт, располагается на одном из углов топосъёмки земельного участка, как правило, нижнем. Эта линейка разделяется на отрезки равного размера.

Точность масштаба

За эталон, который принят картографами для расчёта точности съёмки, взято расстояние в ноль целых одна десятая миллиметра. Это то расстояние на топосъёмке, которое может различить человек без применения различных оптических приборов, например, лупы. Именно по этой причине оно принято за эталонный образец. В качестве примера подсчитаем точность масштаба для топосъёмки 1:500. Как уже говорилось выше, в одном сантиметре этой топосъёмки отображается пятьсот сантиметров реального пространства. Отсюда следует, что в ноль целых одной десятой миллиметра карты будет отображаться пять сантиметров действительно существующего участка земли. Значит, пять сантиметров — это точность топографической съёмки 1:500.

Что такое географический и магнитный азимуты?

Географическим азимутом именуется дирекционный угол, т. е. такой, измерение которого производится горизонтально по часовой стрелке. Отсчет начинается от северного направления меридиана, проходящего через точку пересечения.

Абсолютное значение азимутных линий на топографической основе определяется в пределах 0–360 градусов.

Магнитным азимутом называется горизонтальный угол между базовой линией и северным направлением магнитного меридиана. Направление отсчета схоже с географическим азимутом — также используется ход часовой стрелки.

Ориентация магнитной стрелки может быть изменена. На ее направление влияют:

• особенности местности;
• время проведения замеров.

Определенную сложность в геодезическое ориентирование могут внести магнитные бури. Их вызывают различные причины:

• северное сияние;
• изменение солнечной активности;
• подвижки литосферных плит;
• магнитные аномалии, связанные с техногенными и природными факторами.

Подобные условности ограничивает возможность ориентирования линий по магнитному меридиану. Выбирать данное исходное направление стоит в случае, если высокая точность измерений не является первостепенной задачей.

В рамках замеров могут задействоваться ориентированные углы, привязанные к оси абсцисс в системе прямоугольных координат. При расчете ориентирующего угла применяется северное направление абсциссы или параллельной ей линии. Сформированный ориентированный угол именуется сближением меридианов.

Основные формулы

Зачастую в задачах, касающихся расчёта фигур, необходимо посчитать величину отрезка, лежащего на плоскости. Например, это может быть высота, медиана, биссектриса, радиус или сторона. Основной формулой считается выражение, позволяющее найти расстояние между двумя точками. Если даны две координаты A (x1, y1) и B (x2, y2), то искомое значение определяется по формуле: P (A, B) = ((x2-x1)2 + (y2-y1)2)½.

Если же начало отрезка лежит в нулевой точке, то выражение для вычисления его длины упрощается до вида: P (A, B) = ((x) 2 + (y)2)½, то есть нахождения суммы квадратов чисел, определяющих координаты. Фактически это теорема Пифагора, изучаемая в шестом классе общеобразовательной школы.

Кроме нахождения длины отрезка, к основным формулам относят:

1. Деление отрезков в заданном отношении. Координату C (xc, yc), образованную из A (x1, y1) и B (x2, y2), определяют из соотношения: AC/CB = α1/α2, где α1,2 — действительные числа. Исходя из этого, Xc = (x1α2 + x2α1) / (α1 + α2), Yc = (y1α2 + y2α1) / (α1 + α2). В основе этих формул используется теорема Фалеса.
2. Вычисление угла между векторами. Если есть три точки на плоскости A (x1, y1), B (x2, y2), C (x3, y3), то угол между векторами находится как скалярное произведение, делённое на произведение их длин: cosγ = / |AB| * |AC|. Таким образом, если вектор AB = (x2-x1), (y2-y1), а AC (x3-x1, y3-y1), то C = ((x2-x1) * (x3-x1) + (y2-y1) * (y3-y1)) / ((x2-x1)2 + (y2-y1)2) * ((x3-x1)2 + (y3-y1)2)½.
3. Уравнение прямой. Для его составления нужна координата точки. Фиксирование положения в пространстве задаётся вектором α, которому рассматриваемая прямая перпендикулярна. Задача, по сути, сводится к написанию уравнения прямой, проходящей через точку N0 (x0, y0), перпендикулярную вектору n (A, B). Формула, удовлетворяющая заданию, имеет вид: A (x-x0) + B (y-y0) = 0. Равенство для прямой, проходящей параллельно вектору, пишется как (x-x0)/a = (y-y0)b. Уравнение же, описывающее прямую, проходящую через две точки, имеет вид: (x-x1)/(x2-x1) = (y-y1)/(y2-y1).
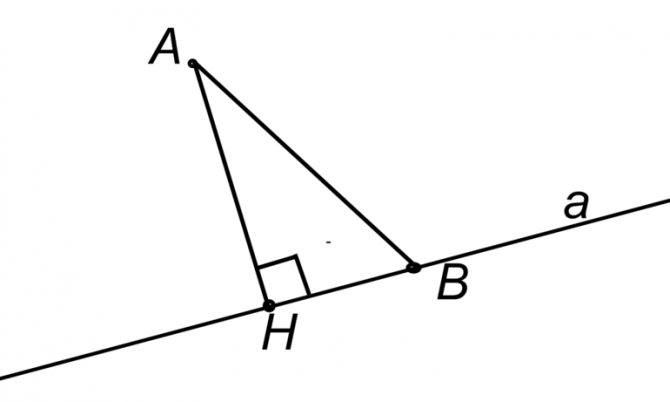
4. Расстояние от точки до прямой. Если имеется точка (x0, y0) и уравнение: Ax+By+C, то расстояние находится из выражения: |Ax0+Byo+C| / (A2+B2)½.

Слайд 14Плоские прямоугольные координатыДля того чтобы можно было пользоваться прямоугольными координатами, на

картах наносятся координатные (километровые) сетки. Для карт М 1 : 10 000 — 1 : 50 000 нанесены квадраты со стороной 1 км; М 1 : 100 000 — квадраты со стороной 2 км.Вертикальные линии сетки параллельны осевому меридиану, а горизонтальные – экватору. Счет горизонтальных километровых линий ведется снизу вверх, а вертикальных – слева направо.Наклон сетки объясняется тем, что западная и восточная линии рамки, представляющие собой географические меридиа­ны, не параллельны осевому меридиану и образуют с ним не­который угол, называемый сближением меридианов. Но так как все вертикальные линии координатной сетки параллельны осе­вому меридиану, то и вся сетка будет наклонена по отношению к вертикальным линиям рамки на такой же угол.

Измерение расстояний и определение площадей по топографической карте, численный, линейный и поперечный масштаб.

Численный масштаб топографической карты.

Это масштаб карты выраженный дробью, числитель которой – единица, а знаменатель – число, показывающее степень уменьшения на карте линий местности. Чем меньше знаменатель масштаба, тем крупнее масштаб карты. Подпись численного масштаба на картах обычно сопровождается указанием величины масштаба – расстояния на местности (в метрах или километрах), соответствующего одному сантиметру карты.

Например 1:50 000 – в 1 сантиметре 500 метров. Величина масштаба в метрах соответствует знаменателю численного масштаба без двух последних нулей. При определении расстояния с помощью численного масштаба линия на карте измеряется линейкой, полученный результат в сантиметрах умножается на величину масштаба.

Линейный масштаб топографической карты.

Линейный масштаб – графическое выражение численного масштаба. Он представляет собой прямую линию, разделенную на определенные части, которые сопровождаются подписями, означающими расстояния на местности.

Линейный масштаб служит для измерения и откладывания расстояний на топографической карте. На рисунке ниже, расстояние между точками А и В равно 1850 метров.

Поперечный масштаб топографической карты.

Поперечный масштаб – график (обычно на металлической пластинке) для измерения и откладывания расстояний на карте с предельной графической точностью (0,1 мм). Стандартный (нормальный) поперечный масштаб имеет большие деления, равные 2 см, и малые деления (слева на графике), равные 2 мм. Кроме того, на графике имеются отрезки между вертикальной и наклонной линиями, равные по первой горизонтальной линии 0,2 мм, по второй – 0,4 мм, по третьей – 0,6 мм и т. д.

С помощью стандартного поперечного масштаба можно измерять и откладывать расстояния на карте любого (метрического) масштаба. Отсчет расстояния по поперечному масштабу состоит из суммы отсчета на основании графика и отсчета отрезка между вертикальной и наклонной линиями. На рисунке выше, расстояние между точками А и В (при масштабе карты 1:100 000) равно 5500 метров (4 км + 1400 м + 100 м).

Измерение расстояний на карте циркулем–измерителем.

При измерении расстояния по прямой линии иглы циркуля устанавливают на конечные точки, затем, не изменяя раствора циркуля, по линейному или поперечному масштабу отсчитывают расстояние. В том случае, когда раствор циркуля превышает длину линейного или поперечного масштаба, целое число километров определяется по квадратам координатной сетки, а остаток – обычным порядком по масштабу.

Измерение расстояний на карте шагом циркуля.

Ломаные линии удобно измерять путем последовательного наращивания раствора циркуля прямолинейными отрезками. Измерение расстояний и длин кривых линий производится последовательным отложением шага циркуля. Величина шага циркуля зависит от степени извилистости линии, но, как правило, не должна превышать 1 см. Для исключения систематической ошибки длину шага циркуля, определенную по масштабу или линейке, следует проверять измерением линии километровой сетки длиной 6–8 см.

Длина извилистой линии, измеренной по карте, всегда несколько меньше ее действительной длины, так как измеряются не кривая линия, а хорды отдельных участков этой кривой. Поэтому в результаты измерений по карте приходится вводить поправку – коэффициенты увеличения расстояний.

Измерение расстояний на карте курвиметром.

Вращением колесика стрелку курвиметра устанавливают на нулевое деление, а затем прокатывают колесико по измеряемой линии с равномерным нажимом слева направо или снизу вверх. Полученный отсчет в сантиметрах умножают на величину масштаба данной карты.

Определение расстояний по прямоугольным координатам точек.

Определение расстояний по прямоугольным координатам точек в пределах одной зоны карты можно произвести по формуле

где D – длина линии, x1, y1 – координаты начальной точки прямой, x2, y2 – координаты конечной точки прямой.

Определение площадей по квадратам километровой сетки карты.

Площадь участка определяется подсчетом целых квадратов и их долей, оцениваемых на глаз. Каждому квадрату километровой сетки соответствует: на картах масштаба 1:25 000 и 1:50 000 – 1 км2, на картах масштаба 1:100 000 – 4 км2, на картах масштаба 1:200 000 – 16 км2.

По материалам книги «Способы автономного выживания человека в природе».Под редакцией Л. А. Михайлова.

Бумажные и электронные карты

Бумажные карты

• легкость
• неприхотливость к условиям использования
• сравнительно низкая цена

• надо уметь сориентировать карту по компасу
• желательно наличие компаса
• не обновляется
• один масштаб

Электронные карты (цифровые карты местности)

Электронные карты — это цифровая модель участка Земной поверхности, сформированная специальными программами.

навигаторах

• есть поиск
• есть расчет примерного маршрута
• обновляются
• компактность
• сами определяют местоположение
• генерализация — отображение в зависимости от масштаба
• можно добавлять «свои» данные, например свои треки, или сканы бумажных карт
• можно записывать свой маршрут

• энергозависимость. Поэтому при длительном походе надо брать запасную батарею (батарейки)
• уязвимость аппаратуры
• высокая цена смартфона или навигатора
• для некоторых программ требуется постоянное подключение к интернету
• некоторые программы бывают платными.

АЗИМУТ

Азимут, магнитный и истинный — угол, образуемый в данной точке на местности или на карте направлением на север и на какой- либо предмет.

Азимутом пользуются для ориентирования при передвижении в лесу, в горах, в песчаной пустыне или в условиях плохой видимости (ночью, при сильном тумане), когда сличить карту с местностью и ориентироваться по ней трудно, а порой и невозможно.

С помощью азимута определяют также направление движения судов в море и самолетов.

На местности отсчет азимутов производится от направления стрелки компаса (ее северного конца) по ходу часовой стрелки от 0° до 360°, иначе говоря — от магнитного меридиана данной точки. Если предмет находится от наблюдателя точно к северу, то азимут его 0°, если на востоке—90°, на юге—180°, на западе — 270°. При наблюдении по компасу измеряется магнитный азимут.

Для определения магнитного азимута компас располагают так, чтобы нулевое деление на циферблате и буква «С» указывали точно на север, т. е. ориентируют компас по сторонам горизонта. Желательно при этом, чтобы компас помещался на высоком пне или на торце вертикально вбитого в землю кола.

Следя за тем, чтобы коробка компаса оставалась неподвижной и стрелка не отходила от нулевого деления, вращают визирное приспособление и наводят мушку на предмет, азимут которого надо определить. Замечают, около какой цифры на лимбе (разделенном на градусы круге) остановился при этом указатель. Отсчет по указателю (в градусах) равен азимуту данного предмета. Если компас не имеет визирного приспособления, его можно заменить тонкой палочкой, которую кладут на стекло компаса так, чтобы она проходила через центр циферблата и была направлена на предмет, азимут которого надо определить.

На рисунке показаны примеры определения азимутов на некоторые местные предметы: на вышку азимут равен 0°, на отдельно стоящее дерево — 50°, на дом — 295°.

Движение по азимуту

. Иногда бывает необходимо дойти до какого-то предмета на местности и возвратиться обратно. Чтобы знать, по какому азимуту следует идти обратно, надо к найденному азимуту прибавить 180°. Получим обратный азимут. Например, если от моста до дерева следует двигаться по азимуту 50°, то обратно—по азимуту 230° (50° +180°=230°). Если при расчете обратного азимута сумма углов окажется больше 360°, то эта величина (360°) отбрасывается. Например, прямой азимут от моста до дома равен 295°, а обратный — 115° (295° +180°-360° = 115°).

Случается, что предмет, до которого необходимо дойти по данному азимуту, не виден наблюдателю (за лесом, холмом). Поступают так. Находят по компасу нужный азимут и стараются отыскать в этом направлении какой-нибудь ориентир (высокое дерево, курган, вышку). Убирают компас и двигаются в направлении ориентира. Дойдя до него, снова определяют этот же азимут и продолжают движение. Бывает, что на пути встретилось болото или озеро. Тогда по компасу определяют нужный азимут и стараются отыскать ориентир на противоположной стороне. Затем компас убирают и движутся в обход встретившегося препятствия. Дойдя до выбранного ориентира, по компасу определяют азимут и продолжают движение.

Двигаясь по лесу, компас держат на ладони перед собой так, чтобы нулевое деление все время совпадало с северным концом стрелки.

Определение азимута по карте

. Азимут определяют и по карте. Предположим, во время похода краеведам надо пройти от лагеря до сторожки лесника, которая находится в 5 км от него. Для определения азимута по карте пользуются транспортиром. В нашем примере азимут от лагеря до сторожки лесника равен 55°. После того как азимут по карте определен, на местности находят его по компасу и идут в нужном направлении.

Азимутальная съемка

. С помощью компаса можно составить план небольшого участка местности. Для этого из какой-то определенной точки (в нашем примере от моста) определяют азимуты до видимых местных предметов, измеряют до них расстояния и данные заносят в таблицу:

Затем на листе бумаги ставят точку, от которой определяли азимуты и расстояния до местных предметов; от нее с помощью транспортира откладывают азимуты и в определенном масштабе расстояния до предметов, которые обозначаются принятыми условными знаками.