Основы туристской деятельности. лекция 8. часть 1

Определение неприступных расстояний

_______ В некоторых случаях, вследствие каких-либо препятствий, измерить линию продольного хода непосредственно лентой невозможно.

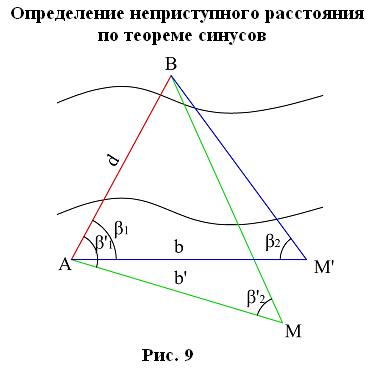
5.1. 1-й случай: (точка В недоступна для линейных измерений). По теореме синусов_______Разбиваем на местности ≈ равносторонний треугольник. Измеряем углы: ß₁ , ß₂ , ß’₁ , ß’₂ и базисы b₁ , b ₂ .
Тогда неприступное расстояние АВ определяется по теореме синусов :

_______1:2000d1:1000среднее из двух определений

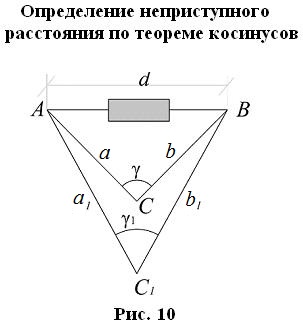
5.2. 2-й случай: разбиваем на местности примерно равнобедренные треугольники ABC, ABC1. По теореме косинусов
_______Этот способ применяется, когда между точками A и В нет взаимной видимости.

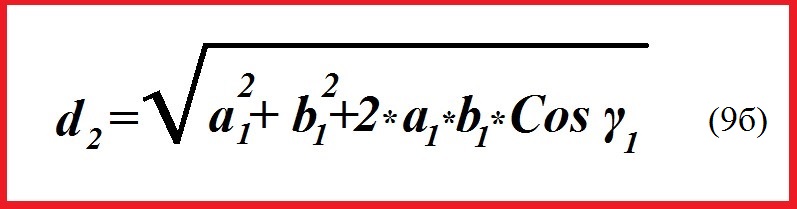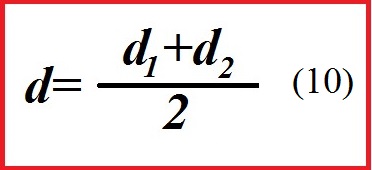aba₁b₁теореме косинусов1/1000

Понятие тысячной и способы измерения её

Тысячная — единица измерения углов, принятая в артиллерии и равняющаяся
одной шеститысячной части оборота. Название происходит от приблизительного
равенства такой единицы измерения углов миллирадиану, то есть тысячной доле
радиана (составляющей 1/(1000 × 2 π) ≈ 1/6283 оборота). Синонимом для этой единицы
измерения угла является малое деление угломера.

Понятие тысячной принято во всех странах мира, и применяется для введения
горизонтальных поправок ведения огня стрелкового оружия и артиллерийских
систем, а также определение расстояний и дистанций. Тысячные записываются и
читаются следующим образом:

тысячная 0-01, читается как ноль, ноль один

тысячных 0-05, читается как ноль, ноль пять

тысячных 0-10, читается как ноль, десять

тысячных 1-50, читается как один, пятьдесят

тысячных 15-00, читается как пятнадцать, ноль ноль

При использовании оптических приборов с делениями в тысячных нужно
учитывать, что есть русская тысячная, которая делит круг на 6000 частей и есть
немецкая тысячная, которая делит круг на 6400 частей.

Исходя из равенства 1 оборота 2π радиан или 360 градусам, существуют
следующие соотношения между всеми этими единицами измерения:

· 1 тысячная ≈ 0,00016(6) оборота

· 1 тысячная ≈ 0,001047 радиана

· 1 тысячная = 0,06 градуса = 3,6 угловой минуты = 3 угл.
минуты 36 угл. секунд

· 1 тысячная = 0,06(6) града

· 1 оборот = 6000 тысячных

· 1 радиан ≈ 954,92 тысячных

· 1 угловая секунда = 0,004629(629) тысячной

· 1 угловая минута = 0,277(7) тысячной

· 1 градус = 16,66(6) тысячных

· 1 град = 15 тысячных

Большим удобством такой нестандартной единицы измерения углов является
хорошая приспособленность к вычислениям линейных и угловых размеров объектов на
местности без каких-либо средств механизации счёта. Пусть объект длиной W
наблюдается с дистанции L под небольшим углом α
(то есть выполняется
условие L >> W, очень часто встречающееся в артиллерийской
практике). Тогда при выражении угла α в радианной мере имеет место:

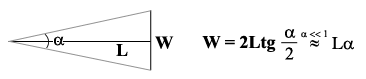
и,
заменяя радианную меру на тысячные, получаем в итоге:

Для
большинства практических расчётов используется приближённый вариант, но в ряде
случаев возникающая при этом погрешность в 4,5 % недопустима и тогда
коэффициент 0,955 не отбрасывается. Упрощённое равенство называется формулой
тысячных. Из этой формулы следует правило для лучшего запоминания соотношения:
«веха высотой 1 метр, удалённая от наблюдателя на 1 километр, видна под углом в
1 тысячную».

Формула
тысячных применима при не слишком больших углах, когда синус угла приближённо
равен самому углу в радианной мере. Условной границей применимости считается
угол в 300 тысячных (18 градусов).

Простейшие способы измерения углов на местности с помощью тысячных.

Углы на местности можно измерять с помощью полевого бинокля, линейки и подручных предметов. В поле зрения бинокля имеются две взаимно-перпендикулярные угломерные шкалы для измерения горизонтальных и вертикальных углов. Величина одного большого деления этих шкал соответствует 0-10, а малого 0-05 тысячных.

Для измерения угла между двумя направлениями надо, глядя в бинокль, совместить какой-либо штрих угломерной шкалы с одним из этих направлений и подсчитать число делений до второго направления. Так, например, отдельноедерево (пулемет противника) расположено влево от дороги на угол 0-30.

Вертикальной шкалой пользуются при определении вертикальных углов. В случае их больших размеров можно пользоваться и горизонтальной шкалой, повернув бинокль вертикально. При отсутствиибинокля углы можно измерять обычной линейкой с миллиметровыми делениями. Если такую линейку держать перед собой на расстоянии 50 см от глаз, то одно ее деление (1 мм) будет соответствовать углу в две тысячных (0-02).

Точность измерения углов таким способом зависит от навыка в вынесении линейки точно на 50 см от глаза. Этого можно достигнуть, привязав к линейке нитку и закусив ее зубами на расстоянии 50 см. С помощью линейки можно измерять углы и в градусах. В этом случае ее следует выносить на расстояние 60 см от глаза. Тогда 1 см на линейке будет соответствовать углу в 1 градус.

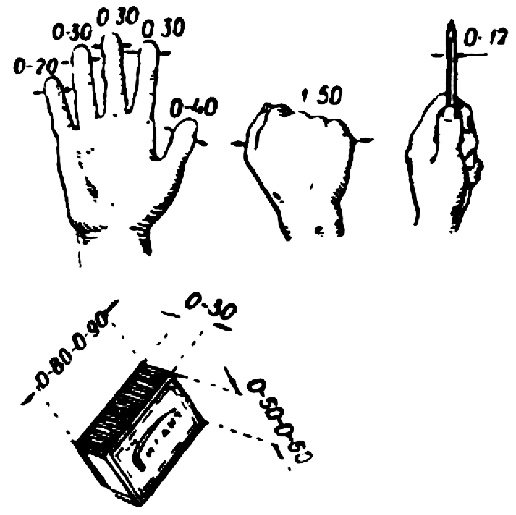
При отсутствии линейки с делениями можно использовать пальцы, ладонь или любой небольшойпредмет (спичечную коробку, карандаш), размер которых в миллиметрах, а следовательно, и в тысячных известен. Такая мерка выносится на расстояние 50 см от глаза и по ней путем сравнения определяется искомая величина угла.

По материалам книги «Карта и компас мои друзья». Клименко А.И.

Виды углов

Есть разные типы углов и у каждого своё название:

острый
прямой
тупой
развернутый
выпуклый
полный

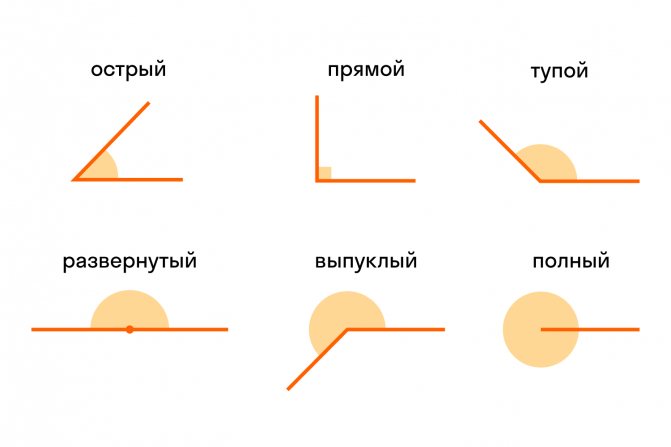
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки

Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого: 90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного: 180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.

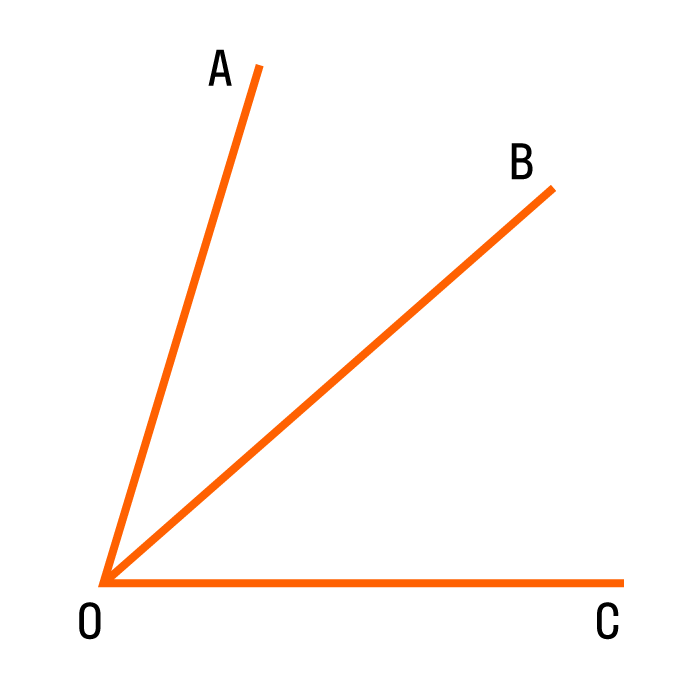
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

∠AOC = ∠AOB − ∠COB,
∠COB = ∠AOB − ∠AOC.

Запоминаем! Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Д = 1000 х В / У

Решим простой пример определения расстояния через формулу тысячной у столба высотой 6 метров вы видите человека. Требуется определить расстояние до него. Вначале определяем, в какой угол укладывается высота столба. Допустим, что высота столба укладывается в угол У=0—05 (пять тысячных). Тогда по формуле для определения дальности получим : Д = 1000 х 6 / 5 = 1200 метров.

Использование двух вышеприведенных формул позволяет определять быстро и точно любые линейные и угловые величины на местности.

Между делениями угломера (в тысячных) и обычной градусной системой угловых мер существуют соотношения : одна тысячная 0-01 равна 3,6′ (минуты), а большое деление угломера (1-00) = 6 градусов. Эти соотношения позволяют при необходимости осуществлять переход от одной системы измерений к другой.

Пример

Вдалеке нам виден человек ростом 165 см. На линейке его рост составляет 3 мм. И тогда, то сколько нам до него идти, рассчитываем по формуле.

Д=(165/3)*5=275 м —м вот такое расстояние между вами и человеком.

Если под рукой нет линейки, можно использовать другие прямые предметы, длину которых вы хорошо знаете. Например, карандаш или коробок со спичками. Измеряется расстояние с помощью подручных предметов тем же вышеописанным способом и с применением тех же данных и методов. Конечно, результат измерений не будет таким же точным, но погрешность будет минимальна.

Ведь даже примерное знание расстояния, которое вам необходимо преодолеть, может выручить вас внештатной ситуации. Вы уже сможете определить, сколько времени вам понадобится для того, чтобы добраться до какого-либо укрытия, если наступает ночь или портится погода. Хватит ли ув вас с собой припасов до того момента, когда в заветной близости окажется населенный пункт.

Пример

Вот таким нехитрым способом можно научиться откладывать расстояние на местности. Этот навык может выручить в том случае, если вы сбились с пути, блуждая по лесам. В армии этот способ широко применяется на практике во время марш-бросков, а также во время стрельбищ, если орудие не оснащено дальним прицелом.

Изначально этот метод и был разработан для использования в полевых условиях, но со временем успешно перекочевал в область туризма. Поэтому, если вы решили отправиться в поход, помимо основных инструментов для определения положения на местности и расстояний, которые необходимо преодолеть, иметь в запасе столь полезное знание никогда не будет лишним. Линейка много места в походном снаряжении не займет.

В пути можно попрактиковаться, сверяя полученный результат с обозначениями на картах. Немного опыта использования такой методики в реальности — и вот вы уже почти матерый профессионал в ориентировании на местности. По крайней мере, неопытные туристы точно будут заглядывать вам в рот, когда вы примените этот способ при них.

Ника

Увлекаюсь походами и путешествиями, фото и видеосъемкой. Хожу в походы с детства. Всей семьей ходили и ездили — то на море, то на речку, на озеро, в лес. Было время, когда в лесу мы проводили по целому месяцу. Жили в палатках, готовили на костре. Наверное, поэтому и сейчас меня тянет в лес и, вообще, на природу. Путешествую регулярно. Примерно три путешествия за год по 10-15 дней и множество 2-х и 3-х дневных походов.

Комментарии: 0Публикации: 668Регистрация: 23-10-2018

Ника Ориентирование

Оптический измеритель расстояния

Такие замеры расстояний с точностью до миллиметра в обычной практике необходимы нечасто. Ведь ни туристы, ни военные разведчики не будут носить с собой габаритные и тяжелые предметы. В основном их используют при проведении профессиональных геодезических и строительных работ. Часто используют при этом такой прибор для измерения расстояния, как оптический дальномер. Он может быть как с постоянным, так и с переменным параллактическим углом и представлять собой насадку к обычному теодолиту.

Измерения производятся по вертикальным и горизонтальным измерительным рейкам, имеющим специальный установочный уровень. Точность измерений такого дальномера достаточно высока, и погрешность может достигать значения 1:2000. Дальность же измерения небольшая и составляет всего лишь от 20 и до 200-300 метров.

Условия задачи и исходные данные

Расстояние между зрачками примерно шесть сантиметров, если человек смотрит прямо вперед и не страдает косоглазием. Расстояние от каждого глаза к поднятому вверх большому пальцу вытянутой руки примерно 60 сантиметров.

Знание этих параметров и оставшихся в памяти сведений из школьного курса геометрии вполне достаточно для определения расстояния до требуемого объекта.

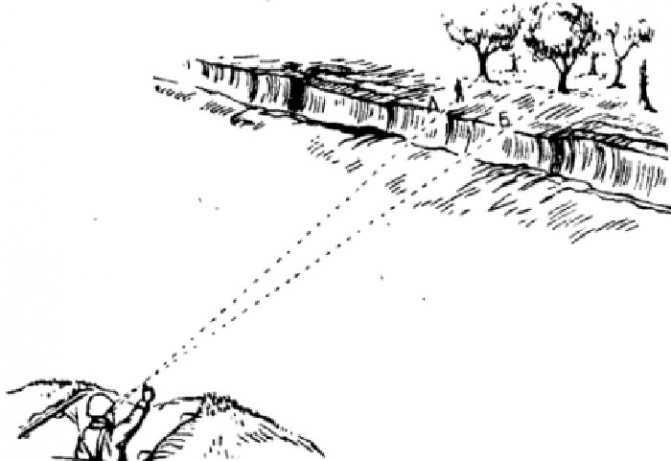
Для определения расстояния до дороги, по которой в это время идет человек, можно воспользоваться двумя способами: по расстоянию между деревьями, которые вдоль дорог высаживают на расстоянии от 3,5 до 5 метров друг от друга, и средней скорости движения человека.

Древние бактерии и их убийц будут искать в вечной мерзлоте ученые из России

Врач рассказал, почему вакцинация способна замедлить скорость старения организма

Обновить гардероб без затрат: модный стилист дал несколько интересных советов

Определение расстояний по угловой величине известных предметов

Пример (рис. 6). Расстояние между телеграфными столбами линии связи, равное 55м (у старых, деревянных, обычно — 50-60 метров интервала, с высотой 6м от земли), покрывается 34 миллиметровыми делениями линейки (3.4см

), удаленной от глаз на50 сантиметров (рука вытянута прямо перед собой). Тогда, расстояние до телеграфной линии, по уравнению соотношения сторон подобных треугольников, равно: Д = 55м * (50см /3.4см ) = 809 м.

Если столбы видны не под прямым углом, а сбоку, тогда, чтобы исключить завышение расстояния до них – надо результат счёта умножить ещё и на поправочный коэффициент: для 45 градусов – 0.7 30° – 0.9

Например, для рассмотренного примера, при расположении линии столбов под углом 45 градусов относительно наблюдателя – реальное расстояние будет: 809 * 0.7 = 566 метров (между 2-мя измеренными столбами). При больших углах – расст-е определяется по высоте опор.

Стандартное расстояние между опорами электросети высокого напряжения (ЛЭП) – 100 метров. Высота заводских труб – 30 м

Если нет линейки, то для измерений можно использовать подручные средства, например – спичечный коробок (5 сантиметров – максимум, 2.5см – до середины).

Точность определения дистанции по угловым величинам составляет 5-10% длины измеряемого расстояния.

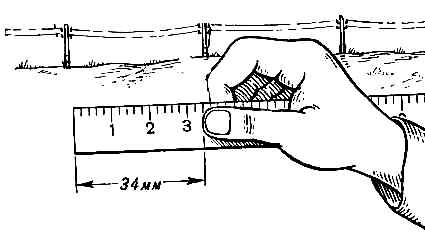
Рис.6

Что такое «ставка»,

Тарифы — всего и больше, чем любые другие единицы использовали плоский угол, равный 1/360 круга, 1/180 прямых углов и 1/90 прямого угла.

Название «степени» происходит от латинского града — деления фрагмента, шаг в тексте, отмеченном (°) (1 ° — 1 градус).

Причины выбора системы. Шестьдесят распределение угловых значений, которые генерируют размеры, единицы измерения неизвестны, но это версия, которая в древнем Вавилоне акадский математический круг делится на шесть равных частей с использованием равностороннего треугольника, который был основой для этого расчета.

Учитывая, что форма шестиугольника широко распространена в естественных структурах, таких как кристаллы (например, типичная форма снежинки) или соты, этот выбор, очевидно, оправдан.

Кроме того, в некоторых старых календарях, особенно в зороастрийском (древнем персидском) и древнем египтяне, продолжительность года составляет 360 дней и 5 дополнительных дней (эпигоменты) считаются священными днями с момента принятия «великого».

Также в течение пяти дополнительных дней ежедневные календари Maya и Aztec 360. Таким образом, вполне возможно, что культурные причины лежат в основе системы в шестидесятые годы.

Способ определения и измерения расстояний на слух.

Ночью в условиях плохой видимости расстояния часто приходится оценивать на слух. Для этого надо уметь определять по характеру звуков их источники и знать, с каких примерно расстояний можно услышать эти звукиночью. При нормальном слухе и благоприятных акустических условиях дальность слышимости можно приближенно считать такой, какой она дана в таблице ниже.

Эти данные меняются в зависимости от конкретных условий, в которых производится наблюдение, поэтому должны учитываться каждым наблюдателем на основе его личного опыта.

По материалам книги «Карта и компас мои друзья». Клименко А.И.

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается ´.

Секунда — 1/60 часть минуты. Обозначается ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.

Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.

Равные углы имеют равную градусную меру.

Как определить расстояние до объекта

Бывают ситуации, когда необходимо уметь определять расстояние до объекта, имея под рукой лишь линейку. К примеру, вы должны рассчитать, через какое время вы доберетесь до видимого вдали населенного пункта или, манящего теплым дымком, домика лесника. Или путеводной звездой для вас стал проходящий вдалеке поезд, и где-то над деревьями вы увидели концы столбов линии электропередач железнодорожных путей.

Современные гаджеты, конечно, никто не отменял: не зря же целые толпы ученых и разработчиков трудились, чтобы внедрить в повседневную (и не очень) жизнь свои изобретения и тем самым облегчить нам существование или поиск выхода в той или иной ситуации. Однако методы и способы, которые уже много десятилетий применяются на практике, не зря до сих пор имеют столь большую популярность.

Способ определения и измерения расстояний на слух.

По материалам книги «Карта и компас мои друзья». Клименко А.И.

Измерение углов на местности с помощью линейки.

Если линейку держать на расстоянии 50 см от глаз, то деление в 1 мм будет соответствовать 0-02. При удалении линейки от глаз на 60 см 1 мм соответствует 6 минутам, а 1 см — 1 градусу. Для измерения угла в тысячныхлинейку держат перед собой на расстоянии 50 см от глаз и подсчитывают число миллиметров между предметами, обозначающими направления сторон угла. Полученное число умножают на 0-02 и получают величину угла в тысячных.

Для измерения угла в градусах порядок действий тот же, только линейку необходимо держать на расстоянии 60 см от глаз. Точность измерения углов с помощью линейки зависит от умения выносить линейку точно на 50 или на 60 см от глаз.

Измерение углов на местности с помощью компаса, по циферблату часов, биноклем со шкалой, с помощью линейки и глазомерное определение углов.

Визирное приспособлениекомпаса предварительно совмещают с начальным штрихом лимба, а затем визируют по направлению левой стороны измеряемого угла и, не меняя положения компаса, против направления правой стороны угла снимают отсчет по лимбу. Это и будет величина измеряемого угла или его дополнение до 360 градусов (60-00), если подписи на лимбе идут против хода часовой стрелки.

Величину угла компасом можно определить более точно, измерив азимуты направлений сторон угла. Разность азимутов правой и левой сторон угла будет соответствовать величине угла. Если разность получится отрицательной, то необходимо прибавить 360 градусов (60-00). Средняя ошибка определения угла этим способом составляет 3-4 градуса.

1.2. Способы определения дальности до цели

Очень часто требуется определять расстояния до различных предметов на местности (дальности до цели). Наиболее точно и быстро расстояния (дальности) определяются посредством специальных приборов (дальномеров) и дальномерных шкал биноклей, стереотруб, прицелов. Но из-за отсутствия приборов нередко расстояния определяют с помощью подручных средств и на глаз.

К числу наиболее точных способов определения дальности (расстояний) до объектов на местности относятся следующие: по угловым размерам объекта и по линейным размерам объектов.

Определение дальности до цели по угловым размерам

предметов (рис. 2) основано на зависимости между угловыми и линейными величинами. Угловые размеры предметов измеряют в тысячных с помощью бинокля, приборов наблюдения и прицеливания, линейки и т. д.

Некоторые угловые величины (в тысячных долях дистанции) приведены в таблице 1.

Расстояние до предметов в метрах определяют по формуле:, где В — высота (ширина) предмета в метрах; У — угловая величина предмета в тысячных.

Например (см. рис. 2):

угловой размер наблюдаемого в бинокль ориентира (телеграфный столб с подпоркой), высота которого 6 м, равен малому делению сетки бинокля (0-05). Следовательно, расстояние до ориентира будет равно: .
угол в тысячных, измеренный линейкой, расположенной на расстоянии 50 см от глаза, (1 мм равен 0-02) между двумя телеграфными столбами 0-32 (телеграфные столбы находятся друг от друга на расстоянии 50 м). Следовательно, расстояние до ориентира будет равно: .
высота дерева в тысячных, измеренная линейкой 0-21 (истинная высота дерева 6 м). Следовательно, расстояние до ориентира будет равно: .

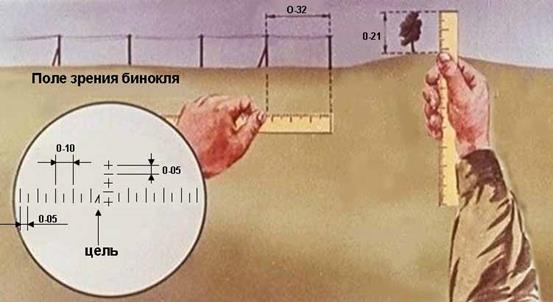
Рис. 2. Определение дальности до цели по угловым размерам объекта (предмета)Таблица 1

Наименование предметов	Размер в тысячных
Толщина большого пальца руки	40
Толщина указательного пальца	33
Толщина среднего пальца	35
Толщина мизинца	25
Патрон по ширине дульца гильзы (7,62 мм)	12
Гильза 7,62 мм по ширине корпуса	18
Карандаш простой	10-11
Спичечная коробка по длине	60
Спичечная коробка по ширине	50
Спичечная коробка по высоте	30
Толщина спички	2

Определение дальности до цели по линейным размерам предметов

заключается в следующем (рис. 3). С помощью линейки, расположенной на расстоянии 50 см от глаза, измеряют в миллиметрах высоту (ширину) наблюдаемого предмета. Затем действительную высоту (ширину) предмета в сантиметрах делят на измеренную по линейке в миллиметрах, результат умножают на постоянное число 5 и получают искомую высоту предмета в метрах. Рис. 3. Определение дальности до цели по линейным размерам объекта (предмета) Например, расстояние между телеграфными столбами равное 50 м (рис.8) закрывается на линейке отрезок 10 мм. Следовательно, расстояние до телеграфной линии равно:

Точность определения расстояний по угловым и линейным величинам составляет 5-10% длины измеряемого расстояния. Для определения расстояний по угловым и линейным размерам предметов рекомендуется запомнить величины (ширину, высоту, длину) некоторых из них, приведенные в табл. 2.

Таблица 2

Предмет	Размеры, м
Высота	Длина	Ширина
Средний танк	2-2,5	6-7	3-3 5
Бронетранспортер	2	5-6	2-2,4
Мотоцикл с коляской	1	2	1,2
Грузовой автомобиль	2-2,5	5-6	2-3,5
Легковой автомобиль	1,6	4	1,5
Пассажирский вагон четырехосный	4	20	3
Железнодорожная цистерна четырехосная	3	9	2,8
Деревянный столб линии связи	5-7	—	—
Человек среднего роста	1,7	—	—

Читать полный конспект Основы управления огнем подразделения

Как с помощью пальца можно узнать расстояние до человека, идущего вдалеке

Порядок решения задачи:

Надо занять такое положение, чтобы направление пути идущего человека было бы перпендикулярным к лучу зрения (или направлению вытянутой руки) человека, определяющего расстояние.
Рука с сжатыми пальцами в кулак (кроме большого пальца, приподнятого наверх), вытягивается вперед и направляется к фигуре идущего человека.
Вытянутую руку следует опереть на какой-нибудь прочный предмет и смотреть по направлению пальца одним глазом (другой глаз на время закрывается; если человек идет слева направо, то сперва закрывается левый глаз, а если человек идет справа налево, то сначала закрывается правый глаз).
Уловив момент, когда человек достигнет точки А (куда направлен луч зрения через палец), необходимо мгновенно закрыть правый глаз и открыть левый. В этот момент палец из точки А переместится направо в точку Б. Если человек идет справа налево, то надо закрыть сперва левый глаз, открыть правый (в этом случае палец сместится налево).
С того момента как палец сместится, вследствие перемены луча зрения, надо сразу же приступить к счету шагов идущего человека и закончить счет, когда пешеход достигнет точки Б.
Определенное таким способом число шагов обратите в метры, для чего помножьте это число на 3 и разделите на 4 (шаг взрослого человека близок к 3/4 метра). Теперь вы узнали расстояние между точками А и Б.
Помножив длину АБ на 10, вы получите окончательный ответ: произведение и есть расстояние от вас до идущего вдалеке человека.

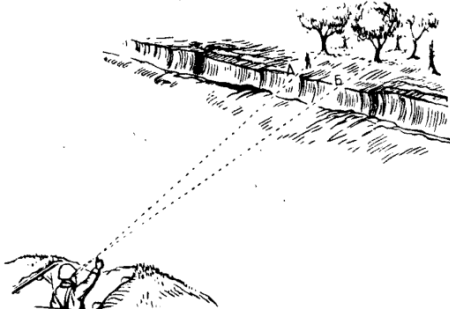
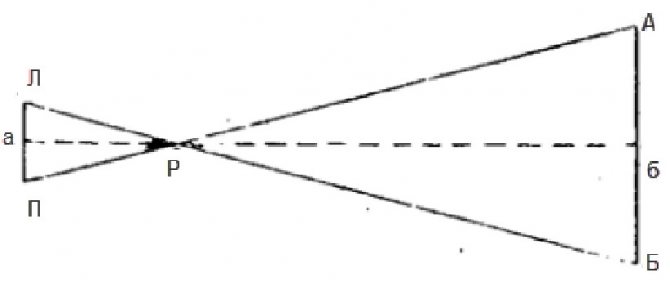
Задача решается на основании подобия треугольников. Обозначения на рисунке:

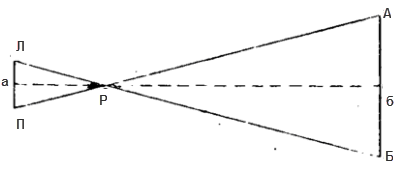
Л — левый глаз измеряющего расстояние,
П — его правый глаз,
Р — вытянутая рука с пальцем,
А — первая метка (определенная направлением прямой линии от правого глаза через палец),
Б — вторая метка (определенная направлением прямой линии от левого глаза через палец).

Из рисунка видно, что треугольники ЛПР и РАБ — подобны. Поэтому: аР/ЛП = Рб/АБ. Высота малого треугольника (аР) равна расстоянию от уровня глаз до пальца вытянутой руки (обычно это расстояние равно 60 см).

ЛП—расстояние между левым и правым глазами (обычно оно равно 6 см). Следовательно, всегда левая часть равенства равна 10*(60/6).

Из правой части мы определили величину АБ. Поэтому понятно, что для того, чтобы узнать величину Рб, надо АБ помножить на 10.

Пример. Человек от точки А до точки Б сделал 40 шагов, что составляет 30 метров (40 * ¾) Следовательно, расстояние до идущего человека в данном случае = 300 метров (30м * 10).

Способ измерения шагами

измерение расстояние видимость размер

Этот метод определения расстояний в боевой обстановке имеет ограниченное
применение

Этот способ применяется обычно при движении по азимуту, составлении схем
местности, нанесении на карту (схему) отдельных объектов и ориентиров и в
других случаях. Счет шагов ведется, как правило, парами. При измерении
расстоянии большой протяженности шаги более удобно считать тройками попеременно
под левую и правую ногу. После каждой сотни пар или троек шагов делается
отметка каким-нибудь способом и отсчет начинается снова. При переводе измеренного
расстояния шагами в метры число пар или троек шагов умножают на длину одной
пары или тройки шагов. Например, между точками поворота на маршруте пройдено
254 пары шагов. Длина одной пары шагов равна 1,6 м.

Тогда Д =254Х1,6=406,4 м.

Обычно шаг человека среднего роста равен 0,7- 0,8 м. Длину своего шага
достаточно точно можно определить по формуле

Д=(Р/4)+0,37,

где Д-длина одного шага в метрах

Р — рост человека в метрах.

Например, если рост человека 1,72 м, то длина его шага

Д=(1,72/4)+0,37=0,8 м.

Более точно длина шага определяется промером какого-нибудь ровного
линейного участка местности, например дороги, протяженностью 200-300 м, который
заранее измеряется мерной лентой (рулеткой, дальномером и т. п.). При
приближенном измерении расстояний длину пары шагов принимают равной 1,5 м.

Средняя ошибка измерения расстояний шагами в зависимости от условий
движения составляет около 2-5% пройденного расстояния.

Счет шагов может выполняться с помощью шагомера (рис.3).

Он имеет вид и размеры карманных часов. Внутри прибора помещен тяжелый
молоточек, который при встряхивании опускается, а под воздействием пружины
возвращается в первоначальное положение. При этом пружина перескакивает по
зубцам колесика, вращение которого передается на стрелки. На большой шкале
циферблата стрелка показывает число единиц и десятков шагов, на правой
малой-сотни, а на левой малой-тысячи. Шагомер подвешивают отвесно к одежде. При
ходьбе вследствие колебания его механизм приходит в действие и отсчитывает каждый
шаг.

Рис.3 Шагомер